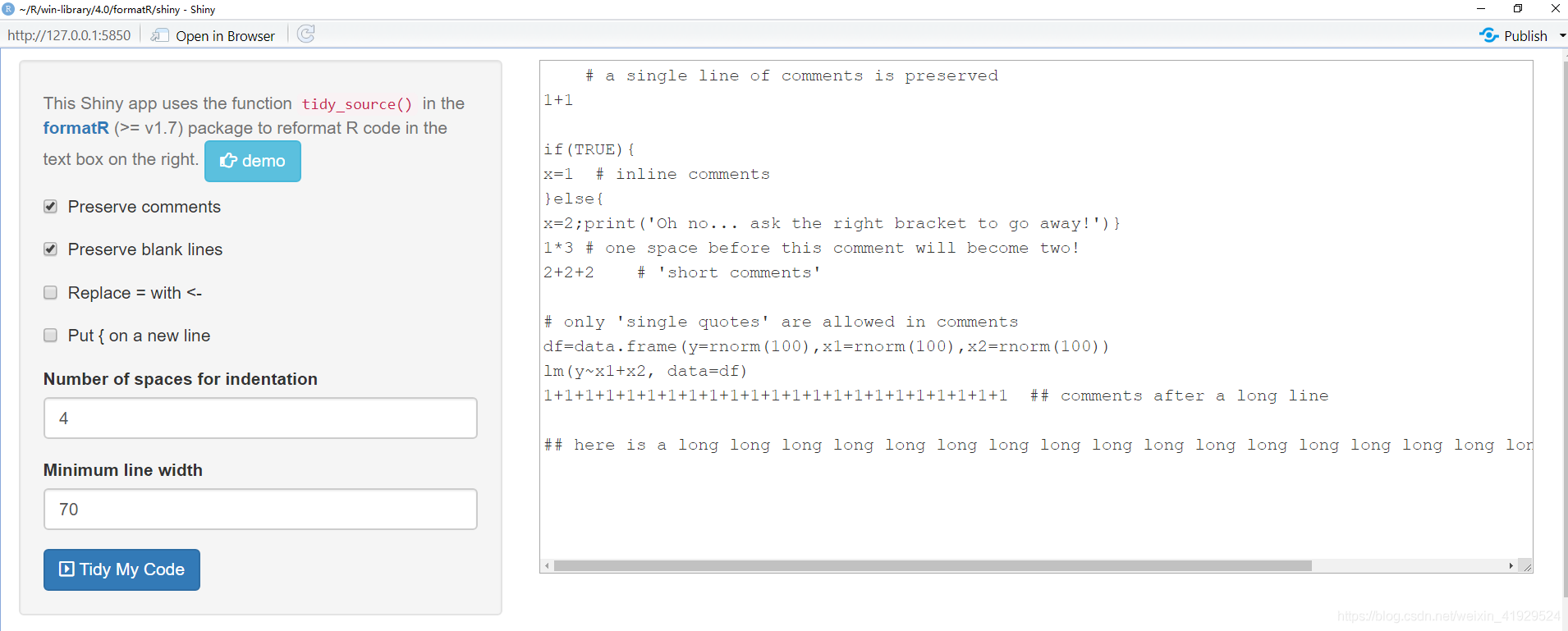
RcppArmadillo几乎和C++中的Armadillo一样,因此本文主要参考Armadillo主页上的手册。
http://arma.sourceforge.net/docs.html
1. 常用数据类型
Mat<type>为模板类,其中type可以是:float, double, std::complex, std::complex, short, int, long, and unsigned versions of short, int, long等。为方便起见,Armadillo C++已经预定义了以下类型。
在Armadillo中,矩阵是按照一列一列(column by column)存在内存中的(column-major ordering)。
| Data Type | Mathematics | Details |
|---|---|---|
| mat, cx_mat | Matrix 矩阵 | Dense real/complex matrix class |
| vec, cx_vec | Column Vector 列向量 | Dense real/complex column vector class |
| rowvec, cx_rowvec | Row Vector 行向量 | Dense real/complex row vector class |
| cube, cx_cube | Cube 3维矩阵 | Dense real/complex cube class (“3D matrix”) |
| field | 域 | Class for storing arbitrary objects in matrix-like or cube-like layouts |
| sp_mat, sp_cx_mat | Matrix 矩阵 | Sparse real/complex matrix class |
| umat/imat | Matrix 矩阵 | Matrix with unsigned/integer elements |
| uvec/ivec | Vector 矩阵 | Vector with unsigned/integer elements |
2. 数学运算
| 算子Operator | 描述 |
|---|---|
| + | Addition of two objects |
| - | Subtraction of one object from another or negation of an object |
| / | Element-wise division of an object by another object or a scalar |
| * | Matrix multiplication of two objects; not applicable to the Cube class unless multiplying a cube by a scalar |
| % | Schur product: element-wise multiplication of two objects |
| == | Element-wise equality evaluation of two objects; generates a matrix of type umat with entries that indicate whether at a given position the two elements from the two objects are equal (1) or not equal (0) |
| != | Element-wise non-equality evaluation of two objects |
| <= | As for ==, but the check is for “greater than or equal to” |
| >= | As for ==, but the check is for “less than or equal to” |
| < | As for ==, but the check is for “greater than” |
| > | As for ==, but the check is for “less than” |
3. 向量、矩阵和域的创建
基本创建
//Matrix: X
mat X(n_rows, n_cols);
mat X(n_rows, n_cols, fill_type);
mat X(size(Y));
mat X(size(Y), fill_type);
mat X("1 0;2 0"); \\create a matrix from a string. (first row is "1 0", second row is "2 0")
cx_mat X(mat,mat); \\for constructing a complex matrix out of two real matrices
//Vector: X
vec X(n_elem);
vec X(n_elem, fill_type);
vec X(size(Y));
vec X(size(Y), fill_type);
cx_vec X(vec,vec); \\for constructing a complex vector out of two real vectors
//Cube or 3-D matrix: X
cube X(n_rows, n_cols, n_slices);
cube X(n_rows, n_cols, n_slices, fill_type);
cube X(size(Y));
cube X(size(Y), fill_type);
cx_cube X(cube, cube); \\for constructing a complex cube out of two real cubes
//Field: F
field<object_type> F(n_elem)
field<object_type> F(n_rows, n_cols)
field<object_type> F(n_rows, n_cols, n_slices)
field<object_type> F(size(X))
//似乎object_type只能是mat或者cube,且不能存储复数类型,比如cx_mat.
//An example of field
mat A(3,4,fill::randu);
vec B(5,fill::randn);
field <mat> F(2,1);
F(0)=A;
F(1)=B;
其中fill_type是可选的,可以是以下选择
| fill_type | 描述 |
|---|---|
| fill::zeros | set all elements to 0 |
| fill::ones | set all elements to 1 |
| fill::eye | set the elements along the main diagonal to 1 and off-diagonal elements to 0 |
| fill::randu | set each element to a random value from a uniform distribution in the [0,1] interval |
| fill::randn | set each element to a random value from a normal/Gaussian distribution with zero mean and unit variance |
用函数创建
| 函数 | 语法 |
|---|---|
| eye() | matrix_type X = eye<matrix_type>(n_rows,n_cols) |
| matrix_type Y = eye<matrix_type>(size(X)) | |
| linspace() | vector_type v = linspace<vector_type>(start,end,N) |
| logspace() | vector_type v = logspace<vector_type>(A, B, N) |
| regspace() | vector_type v = regspace<vector_type>(start, delta, end) |
| ones() | vector_type v = ones<vector_type>(n_elem) |
| matrix_type X = ones<matrix_type>(n_rows,n_cols) | |
| cube_type Q = ones<cube_type>(n_rows,n_cols,n_slices) | |
| some_type R = ones<some_type>(size(Q)) | |
| randi() | vector_type v = rand_type<vector_type>( n_elem, distr_param(a,b)) |
| or randu() | matrix_type X = rand_type<matrix_type>( n_rows, n_cols, distr_param(a,b)) |
| or randn() | matrix_type Y = rand_type<matrix_type>(size(X),distr_param(a,b)) |
| or randg() | cube_type Q = rand_type<cube_type>( n_rows, n_cols, n_slices, distr_param(a,b)) |
注释:
rand_type可以是randi()、randu()、randn()和randg(),分别代表 [a,b] 区间中的整数随机值, U[0,1] 分布中的随机浮点值,从标准正态分布中抽取的随机值,从参数为a,b的Gamma分布中抽取的随机值。distr_param(a,b) 只适用于randi()和randg()。
e.g.
vec v=randu<vec>(5);
regspace()中delta默认是1或-1。
4. 初始化,元素访问,属性和成员函数
4.1. 元素初始化 Element initialization
// C++11
vec v = { 1, 2, 3 };
mat A = { {1, 3, 5},
{2, 4, 6} };
4.2. 元素访问 Element access
无论是向量vec,矩阵mat,立方体cube,还是域field,每个维数均是从0开始的。
| 元素访问 | 描述 |
|---|---|
| (n) | 对于vec和rowvec,访问第n个元素。对于mat和field,首先把矩阵的下一列接到上一列之下,从而构成一个长列向量,并访问第n个元素。 |
| (i,j) | 对于mat和二维field,访问第(i,j)个元素。 |
| (i,j,k) | 对于cube和3D field,访问第(i,j,k)个元素 |
4.3. 子矩阵访问 Submatrix view
矩阵X的连续子集访问
| 函数 | 描述 |
|---|---|
| X.diag(k) | 访问矩阵X的第k个对角线(k是可选的,主对角线为k=0,上对角线为k>0,下对角线为k<0) |
| X.row(i) | 访问矩阵X的第i行 |
| X.col(i) | 访问矩阵X的第i列 |
| X.rows(a,b) | 访问矩阵X从第a行到第b行的子矩阵 |
| X.cols(c,d) | 访问举证X从第c列到第d列的子矩阵 |
| X.submat(a,c,b,d) | 访问矩阵从第a行到第b行和第c列到第d列的子矩阵 |
| X.submat(span(a,b),span(c,d)) | 访问矩阵从第a行到第b行和第c列到第d列的子矩阵 |
| X(a,c, size(n_rows, n_cols)) | 访问矩阵从第a行和第c列开始大小为n_rows和n_cols大小的子矩阵 |
| X(a,c, size(Y)) | 访问矩阵从a行和第c列开始大小和Y相当的子矩阵 |
| X(span(a, b), sel_col) | 访问第sel_col列,从第a行到第b行之间的数据。返回值为向量。 |
| X(sel_row, span(c,d)) | 访问第sel_row行,从第c列到第d列之间的数据。返回值为向量。 |
| X.head_cols( number_of_cols) | 返回头几列 |
| X.head_rows( number_of_rows) | 返回头几行 |
| X.tail_cols( number_of_cols) | 返回尾几列 |
| X.tail_rows( number_of_rows) | 返回尾几行 |
注释:
(1) span(start,end)可以被span::all代替,意味着这一维上所有的元素。
(2) X.diag(k)可以改变第k个对角线的值。
mat X=randn<mat>(4,4);
vec v={1,2,3,4};
X.diag()=v;
向量V的连续子集访问
| 函数 | 描述 |
|---|---|
| V(span(a,b)) | 访问向量V从第a个元素开始到第b个元素结束的子向量 |
| V.subvec(a,b) | 访问向量V从第a个元素开始到第b个元素结束的子向量 |
| V.subvec(a,size(W)) | 访问向量V从第a个元素开始,长度和W相当的子向量 |
| V.head(n_ele) | 访问向量V头几个元素 |
| V.tail(n_ele) | 访问向量V尾几个元素 |
向量或矩阵X的间断子集访问
| 函数 | 描述 |
|---|---|
| X.elem(vector_of_indices) | 向量或者矩阵(按照列向量化以后)中坐标为vector_of_indices的元素;返回向量 |
| X(vector_of_indices) | 向量或者矩阵(按照列向量化以后)中坐标为vector_of_indices的元素;返回向量 |
| X.cols(vector_of_column_indices) | 矩阵X列坐标为vector_of_column_indices的子矩阵;返回矩阵 |
| X.rows(vector_of_row_indices) | 矩阵X行坐标为vector_of_row_indices的子矩阵;返回矩阵 |
| X.submat(vector_of_row_indices, vector_of_column_indices) | 矩阵X行坐标为vector_of_row_indices和列坐标为vector_of_column_indices的子矩阵;返回矩阵 |
| X(vector_of_row_indices, vector_of_column_indices) | 矩阵X行坐标为vector_of_row_indices和列坐标为vector_of_column_indices的子矩阵;返回矩阵 |
立方体(三维矩阵)Q 的切片 slice
| 函数 |
|---|
| Q.slice(slice_number) |
| Q.slices(first_slice, last_slice) |
| Q.subcube(first_row,first_col,first_slice,last_row,last_col,last_slice) |
| Q(span(first_row,last_row),span(first_col,last_col),span(first_slice,last_slice)) |
| Q(first_row,first_col,first_slice,size(n_rows,n_cols,n_slices)) |
| Q(first_row,first_col,first_slice,size(R)) (R is a cube) |
| Q.elem(vector_of_indices) (间断的切片) |
| Q(vector_of_indices) (间断的切片) |
域F的子集访问
| 二维域 2-D Field |
|---|
| F.row( row_number ) |
| F.col( col_number ) |
| F.rows( first_row, last_row ) |
| F.cols( first_col, last_col ) |
| F.subfield(first_row, first_col, last_row, last_col) |
| F(span(first_row, last_row), span(first_col, last_col)) |
| 三维域 3-D Field |
|---|
| F.slice( slice_number ) |
| F.slices( first_slice, last_slice ) |
| F.subfield(first_row, first_col, first_slice, last_row, last_col, last_slice) |
| F(span(first_row,last_row),span(first_col,last_col),span(first_slice,last_slice)) |
4.4. 属性 Attribute
| 属性 | 描述 |
|---|---|
| .n_rows | 行数; 适用于Mat, Col, Row, Cube, field and SpMat |
| .n_cols | 列数;适用于Mat, Col, Row, Cube, field and SpMat |
| .n_elem | 所有元素个数;适用于Mat, Col, Row, Cube, field and SpMat |
| .n_slices | 立方体Cube第三维的维数 |
| .n_nonzero | 非零元素个数;适用于SpMat |
注释:
- 返回值是无符号整数(
uword) - 返回值是read-only的;如果要改变大小(维数),用成员函数
.set_size(),.copy_size(),.zeros(),.ones(), 或者.reset()。
.set_size()
.set_size( n_elem ) .set_size( n_rows, n_cols ) .set_size( n_rows, n_cols, n_slices ) .set_size( size(X) )
.copy_size(A)
把维数设置成和A一样。
.zeros()
.zeros( n_elem ) .zeros( n_rows, n_cols ) .zeros( n_rows, n_cols, n_slices ) .zeros( size(X) )
.ones()
参见.zeros()。
.reset()
把维数设置成0,意味着无元素。
4.5. 其他成员函数 Other member function
| 函数 | 描述 |
|---|---|
| .eye(n,n) / .eye(size(X)) | 创建nxn 单位矩阵;适用于Mat和SpMat |
| .randu(n_elem) | 把向量的值设置成从均匀分布中抽取的随机值 |
| .randu(n_rows,n_cols) | 把矩阵的值设置成从均匀分布中抽取的随机值 |
| .randu(n_rows,n_cols,n_slices) | 把立方体的值设置成从均匀分布中抽取的随机值 |
| .randn() | 与.randu()相同,只不过从正态分布中抽取随机数 |
| .fill(value) | 将Mat, Col, Row, Cube元素设置为value |
| .replace(old_value, new_value) | 可用于替换缺失值:A.replace(datum::nan, 0); 适用于Mat, Col, Row, Cube |
| .transform(lambda_function) (C++11 Only) | 利用lambda函数改变每一个元素的值;适用于Mat, Col, Row和Cube;对于矩阵,按照column-by-column来进行变换;对于立方体,按照slice-by-slice进行变换,每一个slice是一个矩阵。e.g.见此表后注释。 |
| .reshape(n_rows, n_cols) | 适用于矩阵;按照给定的维数建立新的矩阵,转换时,先将旧矩阵按照列转换为长列向量,然后按照给定维数,一列一列地建立新的矩阵。原始结构会被改变。 |
| .reshape(n_rows,n_cols,n_slices) | 适用于立方体;与上类似 |
| .reshape(size(X)) | 适用于矩阵和立方体;与上类似 |
| .resize(n_elem) | 适用于向量;保留原向量结构,增加部分填为0 |
| .resize(n_rows,n_cols) | 适用于矩阵;保留原矩阵结构,增加部分填为0 |
| .resize(n_rows,n_cols,n_slices) | 适用于立方体;保留原立方体结构,增加部分填为0 |
| .resize(size(X)) | 适用于向量、矩阵和立方体 |
| Y.set_imag(X) | 将复数矩阵Y的虚部设置成实数矩阵X |
| Y.set_real(X) | 将复数矩阵Y的实部设置成实数矩阵X |
| .insert_rows() | 插入行 |
| .insert_cols() | 插入列 |
| .insert_slices() | 插入切片 |
| .shed_row()/.shed_rows() | 移除行 |
| .shed_col()/.shed_cols() | 移除列 |
| .shed_slice()/.shed_slices() | 移除切片 |
| .swap_rows( row1, row2 ) | 交换行 |
| .swap_cols( col1, col2 ) | 交换列 |
| .memptr() | 获取对象的指针;适用于Mat,Col,Row和Cube |
| .colptr(col_number) | 获取某一列的指针 |
| iterators | STL-style iterators and associated member functions |
| .t() | 转置或者共轭转置,适用于mat和cx_mat |
| .st() | 普通转置(不取共轭),仅仅适用于cx_mat |
| .i() | 逆矩阵 |
| .min()/.max() | 返回矩阵或立方体的极值;如果是复数,则返回模的极值 |
| .index_min()/.index_max() | 返回矩阵或立方体极值的坐标;返回值为一个无符号整数 |
| .in_range() | 检查给定的坐标或者范围是合法的 |
| .is_empty() | 检查是否为空 |
| .is_square() | 检查是否是方阵 |
| .is_vec() | 检查一个矩阵是否是向量 |
| .is_sorted() | 检查对象是否是被排列过的 |
| .is_finite() | 检查对象是否有限 |
| .has_inf() | 检查是否含有inf值 |
| .has_nan() | 检查是否含有NaN |
| .print() | 打印此对象 |
| .save()/.load() | 向或从文件或流写入或读取对象 |
注释:
.transform(lambda_function)
// C++11 only example
mat A = ones<mat>(4,5);
// add 123 to every element
A.transform( [](double val) { return (val + 123.0); } );
.reshape()和.resize()的区别在于前者不会保存原对象的布局,而后者会保留原对象的布局,且后者更快。例如,如果新对象的维数大于原对象的维数,则新对象中原维数外的元素会被设置成0。
e.g.
mat A = randu<mat>(2,3);
A.reshape(4,4);
[,1] [,2] [,3] [,4]
[1,] 0.02567623 0.8880936 0 0
[2,] 0.12546129 0.6520889 0 0
[3,] 0.52724939 0.0000000 0 0
[4,] 0.30407942 0.0000000 0 0
mat A = randu<mat>(2,3);
A.resize(4,4);
[,1] [,2] [,3] [,4]
[1,] 0.5451790 0.2632051 0.6375933 0
[2,] 0.3753245 0.8050394 0.1627499 0
[3,] 0.0000000 0.0000000 0.0000000 0
[4,] 0.0000000 0.0000000 0.0000000 0
.memptr()
可被用于和一些库交互,比如FFTW。
mat A = randu<mat>(5,5);
const mat B = randu<mat>(5,5);
double* A_mem = A.memptr();
const double* B_mem = B.memptr();
5. 常用函数
5.1. 向量、矩阵和立方体的一般函数
| 函数 | 描述 |
|---|---|
| abs(X) | 求对象元素的绝对值或长度(复数) |
| accu(X) | 求对象所有元素的和 |
| all(X,dim) | 检查向量或者矩阵是否全部元素为非零 |
| any(X,dim) | 检查向量或者矩阵是否至少有一个元素为非零 |
| approx_equal(A,B,method,abs_tol,rel_tol) | 检查A和B中的元素是否近似,近似返回True(Bool值); method可以是absdiff、reldiff和both |
| cond(A) | 返回矩阵A的conditional number |
| conj(X) | 求矩阵或立方体的元素的共轭 |
| conv_to<type>::from(X) | 不同Armadillo矩阵类型之间的转换(e.g. mat和imat);不同立方体之间的转换(e.g.cube和icube);std::vector与Armadillo向量或矩阵之间的转换;将mat转换为colvec, rowvec or std::vector |
| cross(A,B) | 向量叉乘cross product |
| cumsum(X,dim) | 累积加法;如果X是向量,则返回所有元素的和;如果X是矩阵,若dim=0,则返回所有列的和,若dim=1,则返回所有行的和 |
| cumprod(X,dim) | 累积乘法;如果X是向量,则返回所有元素的乘积;如果X是矩阵,若dim=0,则返回所有列的乘积,若dim=1,则返回所有行的乘积 |
| det(A) | 计算方阵的行列式;对于大矩阵,log_det()更加精确 |
| log_det(val,sign,A) | Log determinant of square matrix A; the determinant is equal to exp(val)*sign |
| diagmat(X,k) | 生成新矩阵,用向量X或者矩阵X的对角线元素作为新矩阵的第k个对角线,其他元素设置为零 |
| diagvec(A,k) | 取矩阵A的第k个对角线 |
| dot(A,B)(dot/cdot/norm_dot) | 向量的点乘dot product |
| find(condition) | 返回向量或矩阵满足某条件的元素的坐标向量;e.g. find(A>B)or find(A>0) |
| find_finite(X) | 返回非Inf和NaN的元素的坐标向量 |
| find_nonfinite(X) | 返回是Inf和NaN的元素的坐标向量 |
| find_unique(X,ascending_indices) | 返回X中独一无二的元素;ascending_indices是可选参数,取true(默认)意味着按照递增排列,取false意味着随机排列 |
| imag() / real() | 取复数矩阵虚数或者实数部分 |
| inplace_trans(X,method) / inplace_strans(X,method) | in-place transpose, 相当于 X=X⊺ <script type="math/tex" id="MathJax-Element-4">X=X^\intercal</script>,X的值改变了 |
| is_finite() | 检查是否所有元素都是有限的 |
| join_rows(A,B) / join_horiz(A,B) | 按照水平方向连接两个矩阵 |
| join_cols(A,B) / join_vert(A,B) | 按照垂直方向连接两个矩阵 |
| join_slices(cube_C,cube_D) | 按照第三维连接两个立方体,两个立方体的第一维和第二维的维数必须相等 |
| join_slices(mat_M,mat_N) | 连接两个矩阵构成一个立方体,两个矩阵必须维数相同 |
| join_slices(mat_M,cube_C)/join_slices(cube_C,mat_M) | 将一个矩阵加入一个立方体中 |
| kron(A,B) | Kronecker tensor product |
| min(X,dim) / max(X,dim) | 寻找X在某一维上的极值;X可以是向量(则无dim参数)、矩阵或者立方体;dim是可选参数,0表示返回每一列的极值,1表示返回每一行的极值,2表示返回每一个切片的极值 |
| min(A,B) / max(A,B) | 返回值为一个矩阵或者立方体,其每一个元素代表A和B当中同样坐标的两个元素的最小值和最大值 |
| nonzeros(X) | 返回一个列向量,存储着非零的元素的坐标 |
| norm(X,p) | 计算向量或矩阵的p-norm;向量:p可以是大于等于1的整数,”-inf”,”inf”,”fro”;矩阵:p可以是1,2,”inf”,”fro”,并且此为matrix norm (not entrywise norm);”-inf”是minimum norm, “inf”是maximum norm, “fro”是Frobenius norm |
| normalise(V,p)/normalise(X,p,dim) | 标准化向量V或者矩阵X使其有unit p-norm |
| rank(X,tolerance) | 计算矩阵的秩;tolerance为可选参数 |
| rcond(A) | 矩阵A的conditional number的倒数的估计值;如果接近1代表A是well-conditioned;如果接近0代表A是badly-conditioned |
| repmat(A,num_copies_per_row,num_copies_per_col) | 把矩阵A按照分块矩阵的形式进行复制并生成新的矩阵 |
| shuffle(V)/shuffle(X,dim) | 重新排列向量元素或者矩阵的列或行 |
| sort(V,sort_direction)/sort(X,sort_direction,dim) | 对向量进行排序,或者对矩阵的列(dim=0)或者行(dim=1)中的元素进行排序(默认是列);sort_direction可以是ascend(默认)或者descend |
| sort_index(X,sort_direction) | 返回X按照某顺序排序后的元素的坐标 |
| B=sqrtmat(A)/sqrtmat(B,A) | 矩阵的Complex square root;B是cx_mat |
| sqrtmat_sympd(A)/sqrtmat_sympd(B,A) | 对称矩阵的Complex square root |
| sum(X,dim) | 向量:返回所有元素的和;矩阵:返回每一列(dim=0)或每一行(dim=1)的和;立方体:返回某一维上(第三维是dim=2)的和 |
| trace(X) | 计算矩阵的迹即计算主对角线上元素的和 |
| trans(A)/strans(A) | 矩阵转置;如果是复数矩阵,前者进行的是共轭转置,而后者是直接转置 |
| unique(A) | 返回A的独一无二的元素,并且按照升序排列;如果A是矩阵,则返回一个列向量 |
| vectorise(X,dim) | 将矩阵向量化;如果dim=0,按照column-wise;如果dim=1,按照row-wise |
5.2. 其他一些数学函数
miscellaneous element-wise functions:
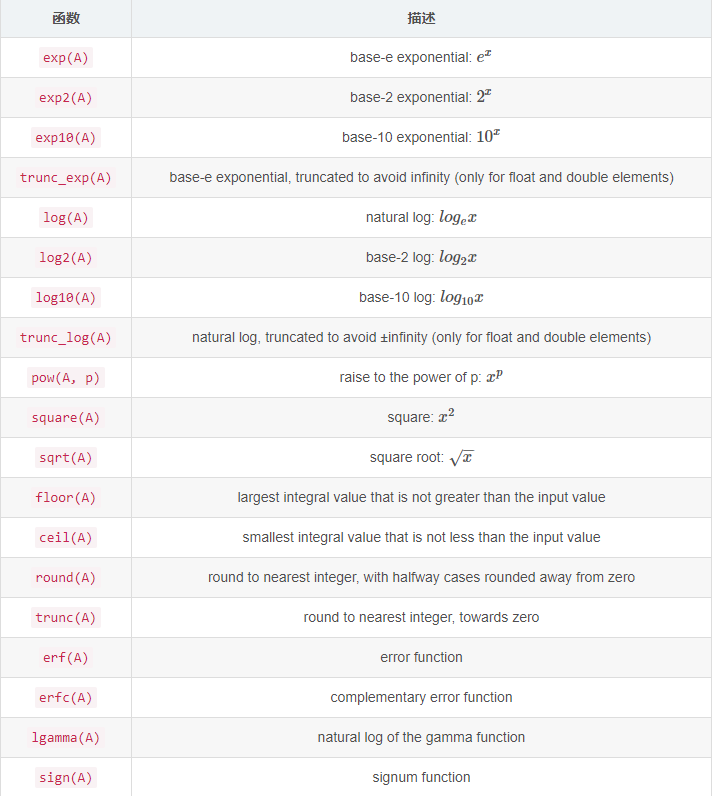
三角函数 Trigonometric element-wise functions (cos, sin, tan, …)
cos, acos, cosh, acosh
sin, asin, sinh, asinh
tan, atan, tanh, atanh
atan2, hypot
5.3. 矩阵的分解、因子化、逆矩阵和线性方程的解
Dense Matrix
| 函数 | 描述 |
|---|---|
| chol | Cholesky decomposition |
| eig_sym | eigen decomposition of dense symmetric/hermitian matrix |
| eig_gen | eigen decomposition of dense general square matrix |
| eig_pair | eigen decomposition for pair of general dense square matrices |
| inv | inverse of general square matrix |
| inv_sympd | inverse of symmetric positive definite matrix |
| lu | lower-upper decomposition |
| null | orthonormal basis of null space |
| orth | orthonormal basis of range space |
| pinv | pseudo-inverse |
| qr | QR decomposition |
| qr_econ | economical QR decomposition |
| qz | generalised Schur decomposition |
| schur | Schur decomposition |
| solve | solve systems of linear equations |
| svd | singular value decomposition |
| svd_econ | economical singular value decomposition |
| syl | Sylvester equation solver |
Sparse Matrix
| 函数 | 描述 |
|---|---|
| eigs_sym | limited number of eigenvalues & eigenvectors of sparse symmetric real matrix |
| eigs_gen | limited number of eigenvalues & eigenvectors of sparse general square matrix |
| spsolve | solve sparse systems of linear equations |
| svds | limited number of singular values & singular vectors of sparse matrix |
5.4. 信号和图像处理
| 函数 | 描述 |
|---|---|
| conv | 1D convolution |
| conv2 | 2D convolution |
| fft / ifft | 1D fast Fourier transform and its inverse |
| fft2 / ifft2 | 2D fast Fourier transform and its inverse |
| interp1 | 1D interpolation |
| polyfit | find polynomial coefficients for data fitting |
| polyval | evaluate polynomial |
5.5. 统计和聚类
| 函数 | 描述 |
|---|---|
| mean(X,dim) | 均值;适用于Vec,Mat,Cube |
| median(X,dim) | 中间值;适用于Vec,Mat |
| stddev(X,norm_type,dim) | 标准差;norm_type可选参数0或1,0代表除以n-1(无偏估计),1表示除以n;适用于Vec,Mat |
| var(X,norm_type,dim) | 方差;适用于Vec,Mat |
| range(X,dim) | 极差;适用于Vec,Mat |
| cov(X,Y,norm_type)/cov(X,norm_type) | 协方差;当两个矩阵X、Y时,矩阵的行表示样本,列表示变量,则cov(X,Y)的第(i,j)-th个元素等于X的第i个变量和Y的第j个变量的协方差; norm_type=0表示除以n-1,norm_type=1表示除以n |
| cor(X,Y,norm_type)/cor(X,norm_type) | 相关系数;与协方差类似 |
| hist/histc | 直方图 |
| princomp | 主成分分析 |
| kmeans(means,data,k,seed_mode,n_iter,print_mode) | K-means聚类,把数据分成k个不相交的集合 |
| gmm_diag | 聚类;Gaussian Mixture Model (GMM) |
以上就是R语言科学计算RcppArmadillo简明手册的详细内容,更多关于RcppArmadillo简明手册的资料请关注好代码网其它相关文章!