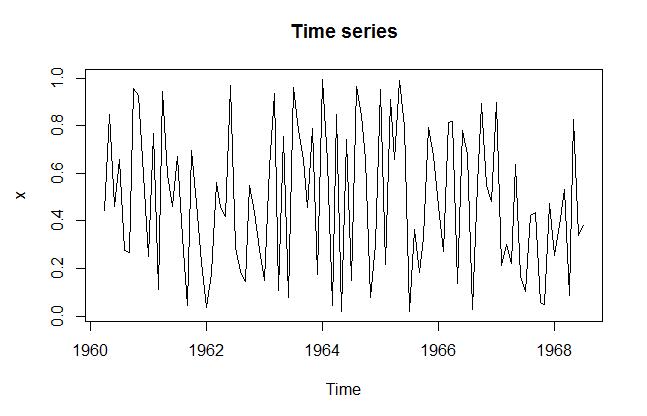
1 连续性

比如下面这个随机函数
x = seq(0,0.1,0.01) y = runif(11,0,1) plot(x,y) lines(x,y)
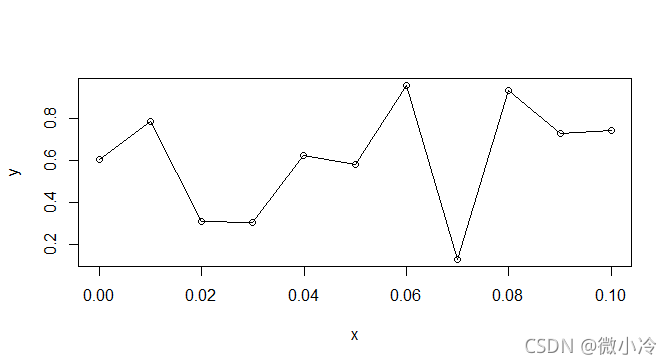

x = seq(0,0.01,0.00001) y = runif(1001,0,1) plot(x,y)
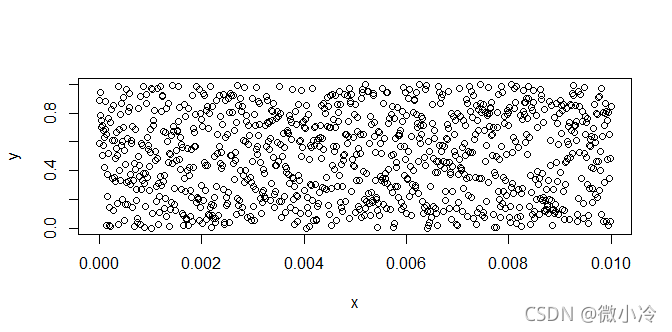
无论我们把区间缩小到什么程度,这种乱糟糟的仿佛要铺满整个坐标图的点的样式并不会发生变化。

也就是说, f(x)从左边趋近于0的时候,f(x)在0处是连续的,而在右侧趋近于0的时候,却并不连续。此即左连续和右连续的概念。
2 求导
回到切线的问题,如果曲线 y=f(x)在 x0点并不连续,那么这点显然没有唯一的一条切线。
有的时候,尽管满足了连续性的要求,也不一定存在切线,比如
y = ∣ x ∣
x = seq(-10,10) y = abs(x) plot(x,y,type='l')
在 x=0的位置,我们找到的切线要么和左边重合,要么和右边重合,也就是说这个函数在x=0处存在两条切线。
同时也就意味着这一点有两个斜率,两个导数。所以,如果把导数定义为某种映射,则一个点只能映射为一个值,所以只能定义这点的导数不存在。

3 数值导数
根据导数的定义,当函数的定义域不连续时,其不连续处显然是不存在导数的,但图形可以“欺骗”我们的眼睛。
> x = seq(-1,1,0.1)
> y = sin(x)
> y1 = cos(x)
> xEnd = x+0.1
> yEnd = y+y1*0.1
> plot(x,y)
> for(i in seq_along(x)){
+ lines(c(x[i],xEnd[i]),c(y[i],yEnd[i]),col="red")
+ }
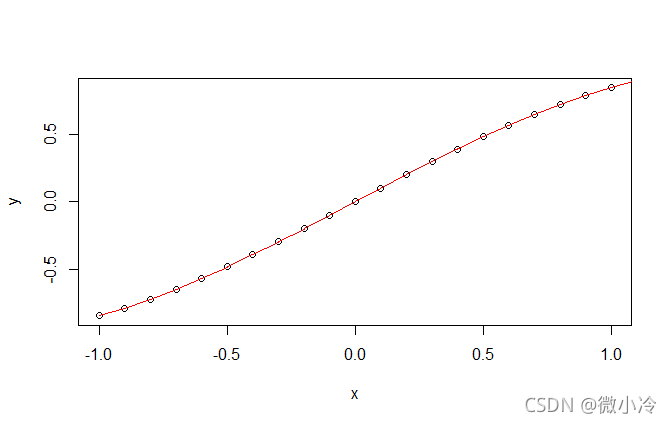
上图中,圆圈是对y = sinx 进行抽样的结果,可以理解为不连续函数;红线则是在每一个分立的点上,sinx在该点的切线。这两者看上去如此一致,说明连续函数的导数在抽样之后仍然具备一定的数学意义。相应地,不连续的函数,也应该有类似于导数一样的存在,从而与连续函数的导数相对应,此即数值导数。如果回顾导数的定义

x = seq(-5,5,0.1) y = cos(x) x1 = seq(-5,5,0.1) end = length(x1) y1 = (sin(x1[2:end])-sin(x1[1:end-1]))/0.1 x5 = seq(-5,5,0.5) end = length(x5) y5 = (sin(x5[2:end])-sin(x5[1:end-1]))/0.5 x10 = seq(-5,5,1) end = length(x10) y10 = (sin(x10[2:end])-sin(x10[1:end-1]))/0.5 plot(x,y,type="l",col="red") lines(x1[2:length(x1)],y1) lines(x5[2:length(x5)],y5) lines(x10[2:length(x10)],y10)
如图所示
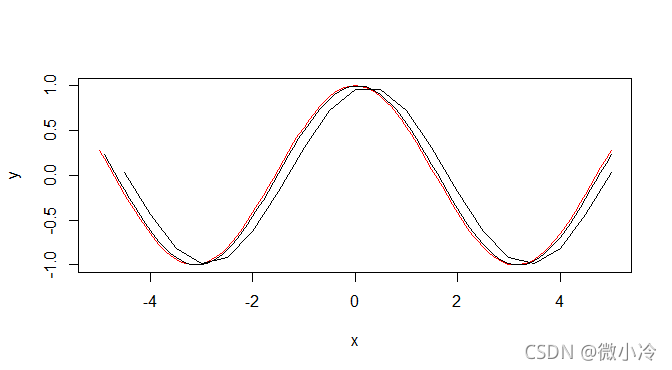
由于我们采用的是后向差分,所以三组差商的值整体右移。此外,随着 h的增大,其误差也越来越明显。
对一个函数进行反复求导,即可得到高阶导数,可以用数学归纳法的方式记为

4 差商与牛顿插值


根据这个表达式,可以通过一个简单的递归程序计算数组的差商
# 差商算法,x,y为同等长度的数组
diffDiv<-function(x,y){
end = length(x)
ind = 2:end #索引
return(
if(end==1) y[1]
else (diffDiv(x[ind],y[ind])
-diffDiv(x[ind-1],y[ind-1]))/(x[end]-x[1])
)
}
如果要计算阶数为k的差商,只需重复调用diffDiv,
kDiffDiv <- function(x,y,k){
len <- length(x)
if(len<k) return(0)
d<-rep(0,len-k)
for(i in 1:(len-k))
d[i] <- diffDiv(x[i:(i+k)],y[i:(i+k)])
return(d)
}
据此,绘制出 y=x^5这个函数的差商,
> plot(x,y) > k = 1 > lines(x[1:(end-k)],kDiffDiv(x,y,k),col="red") > k = 2 > lines(x[1:(end-k)],kDiffDiv(x,y,k),col="green") > k = 3 > lines(x[1:(end-k)],kDiffDiv(x,y,k),col="blue") > k = 4 > lines(x[1:(end-k)],kDiffDiv(x,y,k),col="purple") > k = 5 > lines(x[1:(end-k)],kDiffDiv(x,y,k),col="yellow") > k = 6 > lines(x[1:(end-k)],kDiffDiv(x,y,k),col="gray")
如图所示
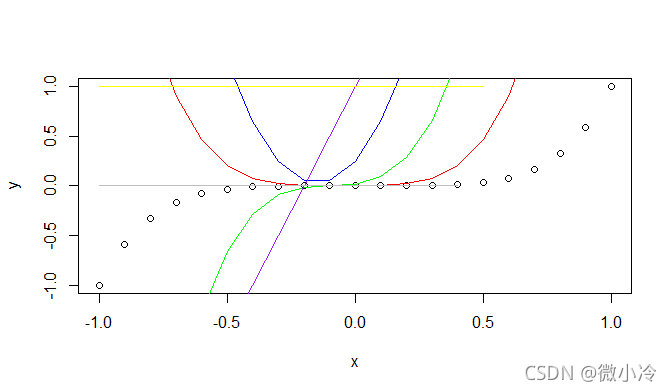
可见差商与微分在阶数上有着一致的趋势。那么,知道了差商之后,可以做点什么呢?
根据差商定义,可得
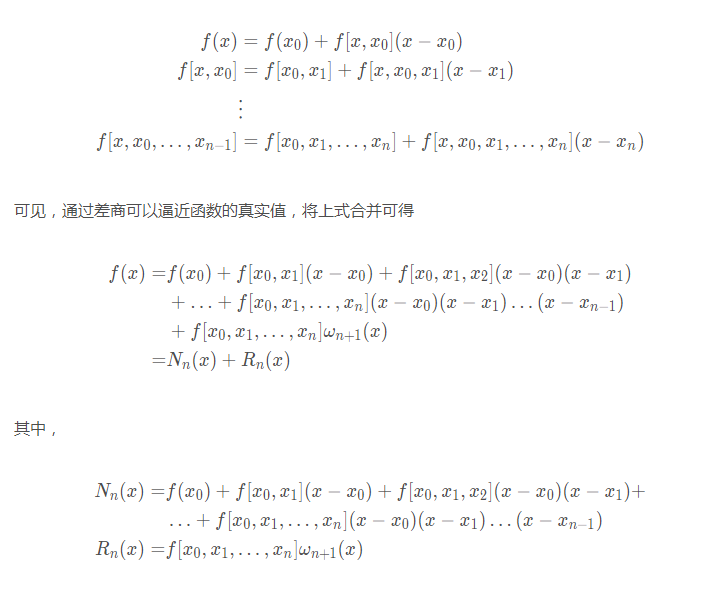

polyMulti<-function(x){
n = length(x)
if(n<2) return(c(-x,1))
omega = rep(0,n+1)
omega[1] = - x[1]
omega[2] = 1
for(i in 2:n){
omega[2:i] = -x[i]*omega[2:i]*+omega[1:(i-1)]
omega[1] = -x[i]*omega[1]
omega[i+1] = 1
}
return(omega)
}
Newton<-function(x,y){
n = length(x)
N = rep(0,n+1)
N[1]=y[1]
for(i in 1:n){
omega = polyMulti(x[1:i])
d = kDiffDiv(x[1:i],y[1:i],i-1)
N[1:i] = N[1:i] + d*omega[1:i]
N[i+1] = d*omega[i+1]
}
return(N)
}
验证一下
x = sort(rnorm(10))
y = x^5+2*x^4
N = Newton(x,y)
Y = y*0
for(i in 1:length(Y))
for(j in 1:length(N))
Y[i] = Y[i]+N[j]*x[i]^(j-1)
plot(x,y)
lines(x,Y)
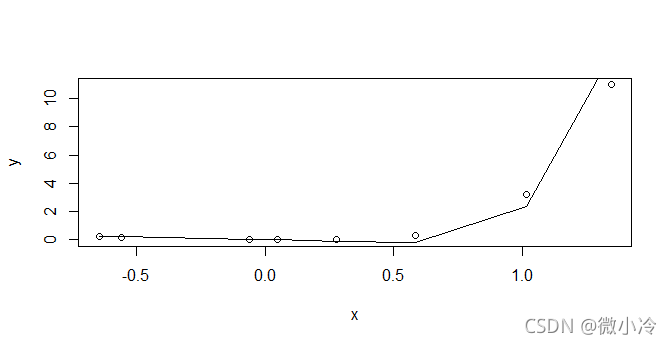
可见效果还是不错的。
5 方向导数

现绘制出100个随机点处x方向的偏导数
x = matrix(data=seq(-5,4.95,0.05),nrow=200,ncol=200)
y = t(x)
z = 1-(x^2+y^2)
library(rgl)
persp3d(x,y,z,col="red")
N = 1000
x0 = rnorm(N)
y0 = rnorm(N)
z0 = 1-(x0^2+y0^2)
x1 = x0+3
z1 = -2*x0*3+z0
for(i in 1:N)
lines3d(c(x0[i],x1[i]),c(y0[i],y0[i]),c(z0[i],z1[i]),col="green")
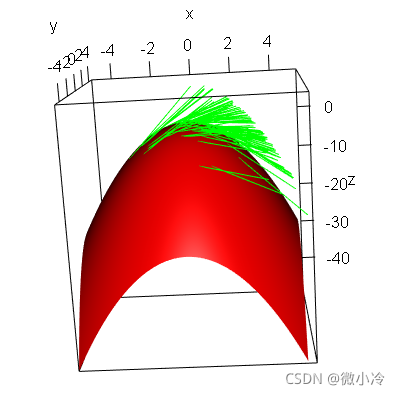
从观感上来看,绿线的确是沿着 x x x方向。但是这个切线显然不是唯一的, y y y轴方向显然存在另一条切线。推而广之,一旦坐标系旋转,那么曲面上任意一点处的 x和 y方向均会发生变化。
那么曲面是否存在一个只和曲面特征有关,而与坐标系无关的参数?
在解决这个问题之前,最好先找到曲面某点沿着任意方向的导数。回顾 x方向偏导数的定义

如果导数的方向发生旋转,则可以写为

如果写成矢量形式,则定义梯度

沿这些点梯度方向做一些直线,看看效果如何
x = matrix(data=seq(-5,4.95,0.05),nrow=200,ncol=200)
y = t(x)
z = -(x^2+y^2)
library(rgl)
persp3d(x,y,z,col="red")
theta = seq(-pi,pi,0.01)
x0 = cos(theta)
y0 = sin(theta)
z0 = 1-(x0^2+y0^2)
x1 = x0*0
y1 = y0*0
z1 = z0+2
for(i in 1:N)
lines3d(c(x0[i],x1[i]),c(y0[i],y1[i]),c(z0[i],z1[i]),col="green")
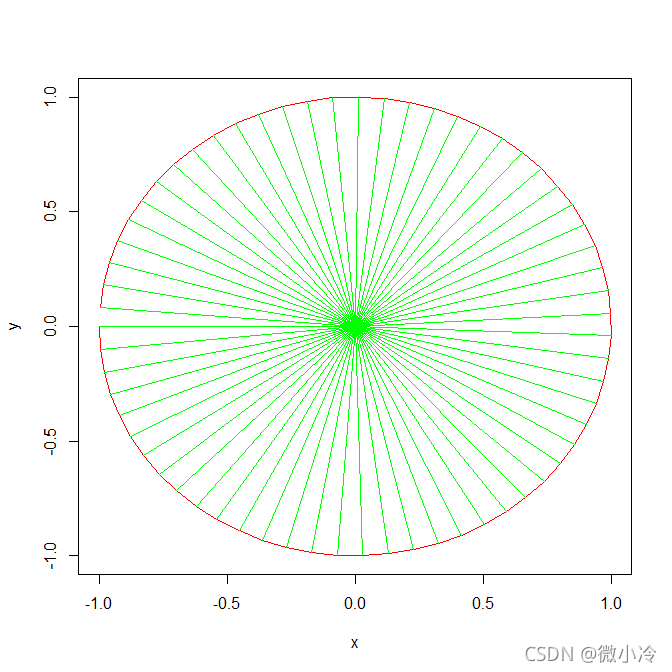
如图所示,像一顶漂亮的帽子,在某个投影方向看去,和我们熟知的切线如出一辙。
6 全微分

做图如下
theta = seq(-pi,pi,0.1)
x = cos(theta)
y = sin(theta)
plot(x,y,type='l',col='red')
x1 = x*0
y1 = (x1-x)/(-2*x)*(-2*y)+y
for(i in 1:length(theta))
lines(c(x[i],x1[i]),c(y[i],y1[i]),col='green')
可见,梯度方向对应的是图形的法线方向。对于二维平面内的曲线而言,其法线方向与切线方向垂直。

回顾偏导数的定义

7 法线

相应地最大方向导数的方向即为梯度的归一化

现随机选择一些点,来绘制一下这四个方向的向量
library(rgl)
N = 1500
x<-rnorm(N)
y<-rnorm(N)
z<-1-x^2-y^2
for(i in 1:N){
lines3d(c(x[i],3*x[i]),c(y[i],3*y[i]),c(z[i],z[i]+1),col='red')
if(y[i]>0.1)
lines3d(c(x[i],x[i]),c(y[i],y[i]-1/y[i]/2),c(z[i],z[i]+1),col='green')
if(x[i]>0.1)
lines3d(c(x[i],x[i]-1/x[i]/2),c(y[i],y[i]),c(z[i],z[i]+1),col='green')
lines3d(c(x[i],x[i]*(1-2*z[i])/(2-2*z[i])),c(y[i],y[i]*(1-2*z[i])/(2-2*z[i])),c(z[i],z[i]+1),col='green')
}

可以看到,绿线几乎重新编织了一遍原函数,而红线则刺破了曲面。
8 偏导数和边缘检测
基于偏导数的边缘检测
灰度图像是天然的z=f(x,y)函数,尽管以一种差分化的形式存在。其中x,y分别代表图像坐标系中的坐标 z可以表示灰度图像的灰度值。
那么接下来我们可以观察一下偏导数作用在图像上是一个什么效果。图片当然是最经典的lena

library(imager)
img = load.image("lena.jpg")
dim(img)
[1] 512 512 1 3
gray = grayscale(img)
par(mfrow=c(1,2))
plot(img)
plot(gray)
可见gray显然为灰度图像,从其维度就能看得出来,然后将其变为二维的数组,接下来就可以进行求导操作了。
dim(gray) [1] 512 512 1 1 mat = array(gray,dim=c(512,512)) mat_x = diff(mat,1) mat_y = t(diff(t(mat),1)) par(mfrow=c(1,2)) image(mat_x) image(mat_y)
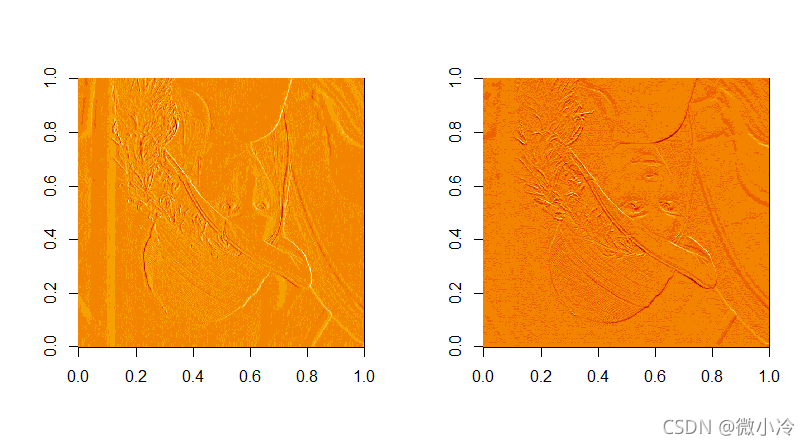
由于图像坐标系默认是从上向下为 y y y轴,从左向右为 x x x轴,所以在我们熟知的坐标系中,图像是上下颠倒的。而且R语言还非常智能(障)地添加了一层伪彩色,这让我们更加清晰地看出,对图像进行差分操作,提取出了边缘信息。
这很容易理解,所谓“边缘”,往往意味着变化较大的点,如果我们抽取lena图的任意一行,
a=mat[256,] par(mfrow=c(1,2)) plot(a,type='l') plot(diff(a,1),type='l')
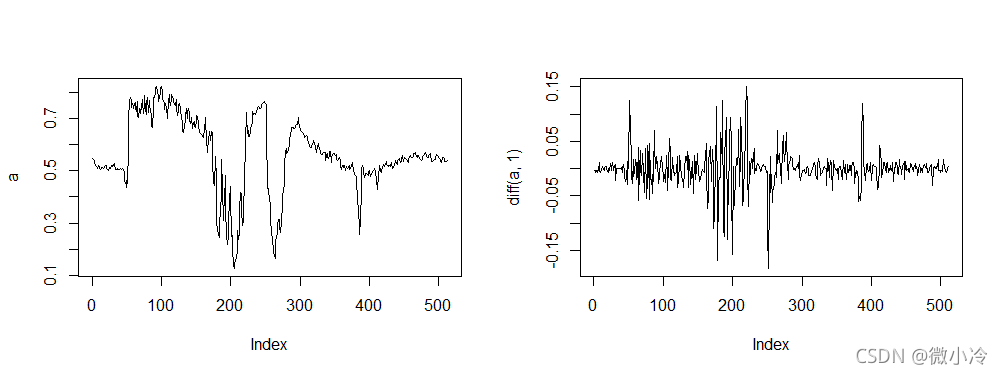
在变化剧烈处,相应地导数较大。
若将偏导数在图像空间中展开,由于任意两个像素点之间的差恒为1,则可得到其差分形式

Roberts算子
求导是对整个函数的定义域展开的一次性操作,但在考察其差分形式之后却发现,数值偏导数可以写成一种对局部区域的反复操作。
例如,就前向差分而言,可以对图像的任意一个子矩阵

theta = c(pi/3,pi/4,pi/5,pi/6) par(mfrow=c(2,2)) for(i in 1:4) image(mat_x[,1:511]*cos(theta[i])+mat_y[1:511,]*sin(theta[i]))
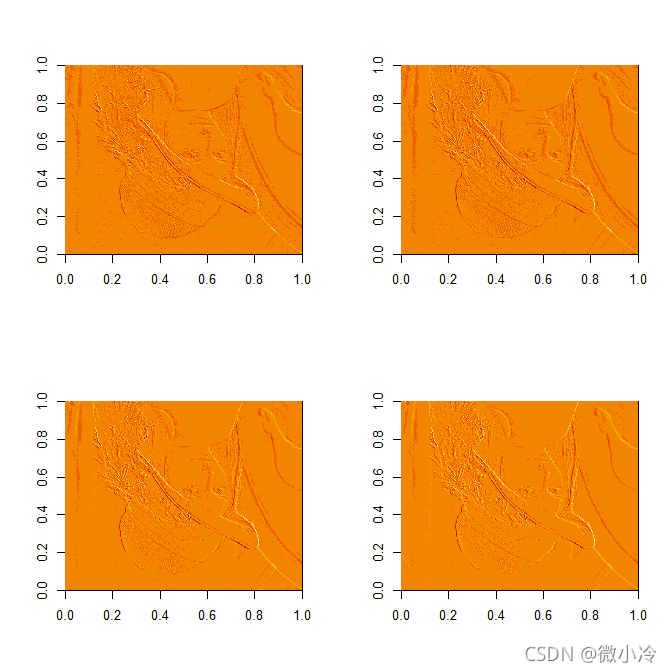
可以看到,最后一张图片的法向角度为 30° ,而其右下角正好有一个 30°附近的清晰的边缘。

其他算子
如果通过中心差分来定义算子,则统一维度后,其x和 y向的梯度算子分别写为

以上就是R语言编程数学分析重读微积分微分学原理运用的详细内容,更多关于R语言数学分析微分学原理的资料请关注好代码网其它相关文章!