一 理解极限
二 微分学
泰勒级数
如果我是泰勒,我会把思考的起点建立在这样的一个等式上那么接下来我们直观地感受一下Taylor级数时如何逐渐逼近某个函数的。简
泰勒级数
如果我是泰勒,我会把思考的起点建立在这样的一个等式上


那么接下来我们直观地感受一下Taylor级数时如何逐渐逼近某个函数的。简单起见,在此选择 sinx作为被拟合的函数。
library(ggplot2)
library(gganimate)
library(av)
library(tibble)
x = seq(-pi,pi,0.1)
n = length(x)
xs = rep(x,11)
ys = rep(sin(0),n)
ts = rep(0,n)
for(i in 1:10){
y <- if(i%%2==0) 0 else 1
if((i-1)%%4>1)
y = -y
y = y/factorial(i)*x^i
m = length(ys)
y = y+ys[(m-n+1):m]
ys = c(ys,y)
ts = c(ts,rep(i,n))
}
data<-tibble(x=xs,y=ys,t=ts)
ggplot(data,aes(x,y))+geom_point()+transition_time(t)+ease_aes('linear')
如图所示
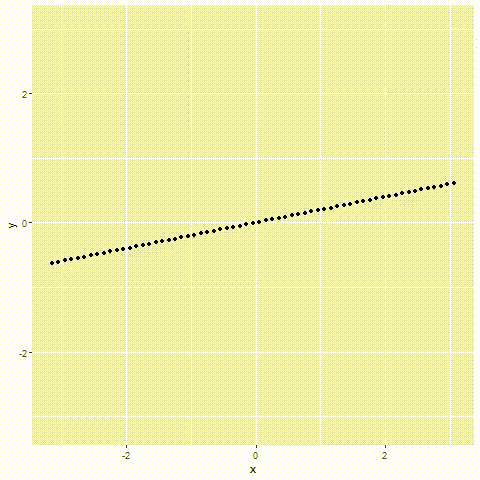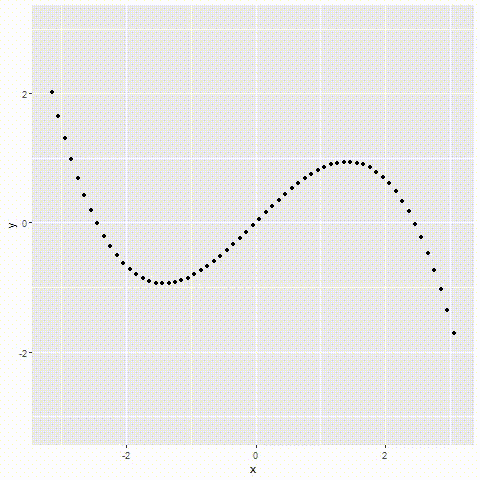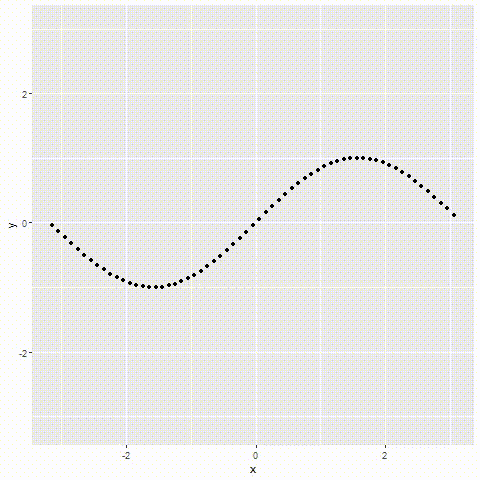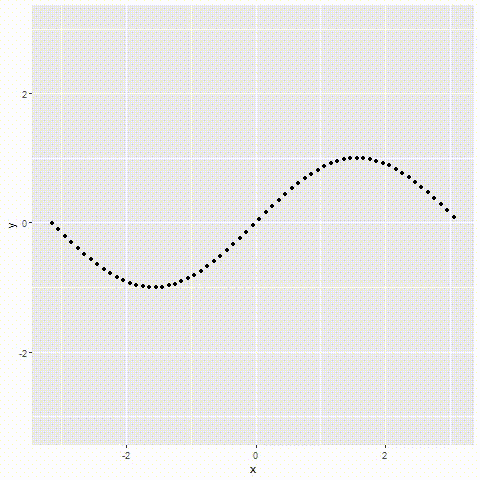
以上就是R语言编程重读微积分泰勒级数示例详解的详细内容,更多关于R语言编程微积分泰勒级数的资料请关注好代码网其它相关文章!