这道数学题怎么做
最新回答
不问归期
2025-02-24 04:03:38
分析:
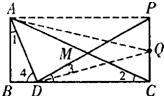
(1)根据AB=2,BD=1,∠B=90°,根据勾股定理得到AD的长,根据∠BAD=∠ACB得到sin∠ACB=sin∠BAD,在Rt△ABD中,根据三角函数的定义就可以求出sin∠ACB的值.
(2)设MC=x,则DM=x,AM=AC-MC=2√5-x,在Rt△ADM中,由勾股定理就可以求出CM的长.
(3)根据四边形ADQP的面积等于四边形ABCQ的面积,就可以求出t的值.
解:
(1)在Rt△ABD中,根据勾股定理得到AD=√5,sin∠ACB=sin∠BAD= BD/AD=√5/5.
(2)MD=MC
设MC=x,则DM=x,AM=AC-MC=2√5-x
在Rt△ADM中,由勾股定理得x=3√5/4
∴CM=x=3√5/4
(3)连接AP、AQ、DQ
t= 6/7
∴当点Q从点c向点P运动4s/7时,存在四边形ADQP的面积等于四边形ABCQ的面积.
希望对你有帮助,祝你学习进步。
追问
第三小题详细说一下!
追答
是用△abd的面积+△dcq的面积=△apq的面积的等量关系,求出来的。速度是1个单位,根据时间t可求出长度t,再列方程解出t
S△DCP=CD*CQ/2=3t/2
S△APQ=PQ*BC/2=2(CP-t)=2(√(45/4-9)-t)=2(3/2-t)=3-2t
S△ABD=AB*BD/2=1
列方程1+3t/2=3-2t,两边同乘以2
2+3t=6-4t
7t=4
t=4/7
上面t=6/7笔误。
姐↗就是女汉子
2025-02-24 08:53:51
ad/ac=bd/ab
且ab=2;bd=1;ad=√5
所以ac=2√5
Sin∠acb=2/(2√5)=√5/5
2) ∠b=90°,∠adm=90°
且 ∠adm+∠mdc=∠b+∠bad
所以 ∠mdc=∠bad
已知∠acb=∠bad
所以 ∠mdc=∠acb
Sin∠mdc=Sin∠acb=√5/5;Cos∠mdc=√(1-1/5)=(2√5)/5
因此 md=mc
又∠p+∠mdc=∠mcp+∠acb=90°
所以 ∠p=∠mcp
即 mc=mp=md
在△abc中bc=√(20-4)=√16=4
所以dc=bc-bd=4-1=3
△dcp中,Cos∠mdc=dc/dp
所以3/dp=(2√5)/5
dp=(3√5)/2
mc=mp=md=dp/2=(3√5)/4
3)设时间为t时两个四边形面积相等
即此时△abd的面积+△dcq的面积=△apq的面积
而△abd面积=(1/2)ab×bd=1
△dcq面积=(1/2)dc×cq=(1/2)×3×t=(3/2)×t
△apq面积=(1/2)pq×bc=(1/2)×4×(pc-t)=2(pc-t)
其中pc=√(45/4-9)=√(9/4)=3/2
所以得到方程1+(3/2)t=2(3/2-t)
(3/2+2)×t=3-1
(7/2)×t=2
t=4/7
即当经过4/7单位时间后,cq=4/7时。
两个四边形的面积相等。
纯洁的小黄瓜
2025-02-24 11:11:27
看不清里的字啊
热门标签
