简单解释各种运算符及其关系?
2024-12-01 14:05:59
例如加号曾经有好几种,现代数学通用“+”号。“+”号是由

也有人说,卖酒的商人用“-”表示
到了十五世纪,德国数学家魏德美正式确定:“+”用作加号,“-”用作减号。
乘号曾经用过十几种,现代数学通用两种。一个是“×”,最早是英国数学家奥屈特1631年提出的;一个是“·”,最早是英国数学家赫锐奥特首创的。德国数学家
到了十八世纪,美国数学家欧德莱确定,把“×”作为乘号。他认为“×”是“+”的旋转变形,是另一种表示增加的符号。
“÷”最初作为减号,在欧洲大陆长期流行。直到1631年英国数学家奥屈特用“:”表示除或比,另外有人用“-”(除线)表示除。后来瑞士数学家拉哈在他所著的《代数学》里,才根据群众创造,正式将“÷”作为除号。
平方根号曾经用拉丁文“Radix”(根)的首尾两个字母合并起来表示,十七世纪初叶,法国数学家
十六世纪法国数学家维叶特用“=”表示两个量的差别。可是
1591年,法国数学家韦达在菱形中大量使用这个符号,才逐渐为人们接受。十七世纪德国莱布尼茨广泛使用了“=”号,他还在几何学中用“∽”表示相似,用“≌”表示全等。
任意号(全称量词)∀来源于英语中的Arbitrary一词,因为小写和大写均容易造成混淆,故将其单词首字母大写后倒置。同样,存在号(存在量词)∃来源于Exist一词中E的反写。
运算符号
如加号(+),减号(-),乘号(×或·),除号(÷或/),两个集合的并集(∪),交集(∩),根号(√ ̄),
关系符号
如“=”是等号,“≈”是近似符号(即约等于),“≠”是不等号,“>”是大于符号,“<”是小于符号,“≥”是大于或等于符号(也可写作“≮”,即不小于),“≤”是小于或等于符号(也可写作“≯”,即不大于),“→ ”表示变量变化的趋势,“∽”是相似符号,“≌”是全等号,“∥”是平行符号,“⊥”是垂直符号,“∝”是正比例符号(表示反比例时可以利用倒数关系),“∈”是属于符号,“⊆”是包含于符号,“⊇”是包含符号,“|”表示“能整除”(例如a|b 表示“a能整除b”,而
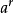
||b表示r是a恰能整除b的最大幂次),x,y等任何字母都可以代表未知数。
结合符号
如小括号“()”,中括号“[ ]”,大括号“{ }”,横线“—”,比如
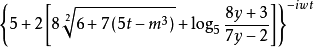
。
性质符号
如正号“+”,负号“-”,正负号“
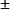
”(以及与之对应使用的负正号“

”)
省略符号
如三角形(△),

∵ 因为
∴ 所以
总和,连加:∑,求积,连乘:∏,从n个元素中取出r个元素所有不同的

(n元素的总个数;r参与选择的元素个数),幂
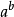
等。
希望我能帮助你解疑释惑。
热门标签
