人工智能 基于知识的智能体

先引用一段资料

------------------------------------------------------------------

第一类包括符号处理的方法。它们基于N e w e l l和S i m o n的物理符号系统的假说。尽管不是所有人都赞同这一假说，但几乎大多数被称为“经典的人工智能”（即哲学家John Haugeland所谓的“出色的老式人工智能”或G O FA I）均在其指导之下。这类方法中，突出的方法是将逻辑操作应用于说明性知识库。最早由John McCarthy 的“采纳意见者”备忘录提出[ M c C a r t h y1 9 5 8 ]，这种风格的人工智能运用说明语句来表达问题域的“知识”，这些语句基于或实质上等同于一阶逻辑中的语句。采用逻辑推理可推导这种知识的结果。这种方法有许多变形，包括那些强调对逻辑语言中定义域的形式公理化的角色的变形。当遇到“真正的问题”，这一方法需要掌握问题域的足够知识，通常就称作基于知识的方法。许多系统的构建都运用了这些方法，在本书后面将会提到一些。

在大多数符号处理方法中，对需求行为的分析和为完成这一行为所做的机器合成要经过几个阶段。最高阶段是知识阶段，机器所需知识在这里说明。接下来是符号阶段，知识在这里以符号组织表示（例如列表可用列表处理语言L I S P来描述），同时在这里说明这些组织的操作。接着，在更低级的阶段里实施符号处理。多数符号处理采用自上而下的设计方法，从知识阶段向下到符号和实施阶段

----------------------------------------------------------------

题目的意思就是叫你根据以知识为基础的原则解题

比如，程序由无限多个判断组成，这些判断的条件就是所谓的知识。像是刺激响应一样。比如，玩家一方派兵到了AI方的城下，这是一种情况，你应该为你的AI写下该怎么做的脚本。懂了吗？

举个例子

--------------------------------------------------------------

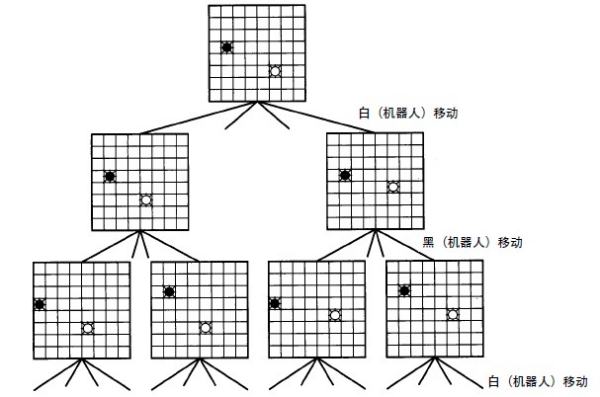
以图中的网格为例，两个机器人，分别命名为“b l a c k”和“w h i t e”。它们可以向其所在的行或列中的相邻一格交替地移动（比如说， w h i t e先移动），而且轮到其中一个时，它必须移动。假设w h i t e的目标是与b l a c k在同一格，而b l a c k的目标是避免发生这种情况。w h i t e就可建立一棵搜索树，在交替的级别上，b l a c k可能的行动也被考虑进去。我上传的图中画出了这棵搜索树的一部分。

为了选取最佳的起始动作， w h i t e需要分析这棵树来决定可能的结果——即：考虑b l a c k会阻止w h i t e实现此目标。在这种冲突的情况下，一个a g e n t可能发现一步移动，使得无论对方如何移动，它都可达到目标。不过更常见的情况是，由于计算和时间的限制，无论哪方都不能找到一个动作以保证取得成功。本书将提供有限范围搜索方法，可用于在这种情况下找到合理的移动方式。在任何情况下，在决定了第一步之后，执行移动，考虑另一方的可能移动，然后在感知/计划/动作方式中重复计划过程。

这个网格例子是双a g e n t、信息完全，零和（z e ro - s u m）博奕的一个实例。此处所讨论的是，两个a g e n t（称为博弈者）轮流移动，直到其中任何一方获胜（另一方因此失败），或双方和局。

每个博弈者完全熟悉环境及自己和对方可能的移动方式和影响（尽管每个博弈者都不知道另一方在任何情况下究竟会怎样移动）。研究这种博弈可使我们深入了解当有多个a g e n t时，计划过程可能出现的更多的普遍问题—即使在这些a g e n t的目标并不互相冲突时。

可以看出，有许多常见的博弈，包括国际象棋、西洋跳棋( d r a n g h t )和围棋，都属于这种类型。而且它们的程序已经编写得相当好——有的甚至可以达到参赛的水平。但此处，以并不十分有趣的井字博弈（Ti c - Ta c - To e）为例，因为它简单，有利于分析搜索技巧。有些博弈（例如

西洋双陆棋，B a c k g a m m o n）由于包含了概率因素而导致难以对它们进行分析。对许多博弈，特别像国际象棋这一类，通常都用图标来描述自己的状态空间，我们用8×8数组来记录黑白机器人在8×8网格中的不同位置；用算子表示博弈的移动，算子把一种状态描述转换为另一种描述，由一个开始节点和每个博弈者的算子隐式定义博弈图，照前面章节的

方法建立搜索树，但在选择第一步时要使用一些不同方法。

-----------------------------------------------------------------

加不加分我到不奢求，但我希望以后多交流，我也喜欢人工智能