随机数和蒙特卡洛模拟求解单一变量非线性方程求解线性系统方程函数的数学积分常微分方程的数值解
等势线绘图和曲线:
等势线 import numpy as np
i
- 随机数和蒙特卡洛模拟
- 求解单一变量非线性方程
- 求解线性系统方程
- 函数的数学积分
- 常微分方程的数值解
等势线绘图和曲线:
等势线 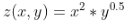
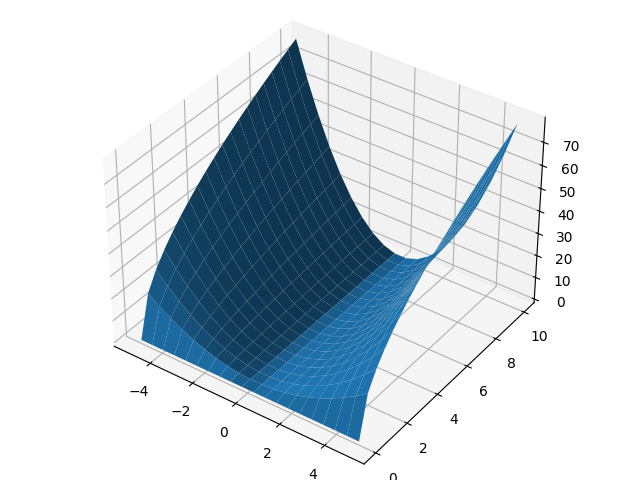
import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D x_vals = np.linspace(-5,5,20) y_vals = np.linspace(0,10,20) X,Y = np.meshgrid(x_vals,y_vals) Z = X**2 * Y**0.5 line_count = 15 ax = Axes3D(plt.figure()) ax.plot_surface(X,Y,Z,rstride=1,cstride=1) plt.show()
非线性方程的数学解:
- 一般实函数 Scipy.optimize
- fsolve函数求零点(限定只给实数解)
import scipy.optimize as so
from scipy.optimize import fsolve
f = lambda x:x**2-1
fsolve(f,0.5)
fsolve(f,-0.5)
fsolve(f,[-0.5,0.5])
>>>fsolve(f,-0.5,full_output=True)
>>>(array([-1.]), {'nfev': 9, 'fjac': array([[-1.]]), 'r': array([1.99999875]), 'qtf': array([3.82396337e-10]), 'fvec': array([4.4408921e-16])}, 1, 'The solution converged.')
>>>help(fsolve)
>>>Help on function fsolve in module scipy.optimize._minpack_py:
fsolve(func, x0, args=(), fprime=None, full_output=0, col_deriv=0, xtol=1.49012e-08, maxfev=0, band=None, epsfcn=None, factor=100, diag=None)
Find the roots of a function.
Return the roots of the (non-linear) equations defined by
``func(x) = 0`` given a starting estimate.
Parameters
----------
func : callable ``f(x, *args)``
A function that takes at least one (possibly vector) argument,
and returns a value of the same length.
x0 : ndarray
The starting estimate for the roots of ``func(x) = 0``.
args : tuple, optional
Any extra arguments to `func`.
fprime : callable ``f(x, *args)``, optional
A function to compute the Jacobian of `func` with derivatives
across the rows. By default, the Jacobian will be estimated.
full_output : bool, optional
If True, return optional outputs.
col_deriv : bool, optional
Specify whether the Jacobian function computes derivatives down
the columns (faster, because there is no transpose operation).
xtol : float, optional
The calculation will terminate if the relative error between two
consecutive iterates is at most `xtol`.
maxfev : int, optional
The maximum number of calls to the function. If zero, then
``100*(N+1)`` is the maximum where N is the number of elements
in `x0`.
band : tuple, optional
If set to a two-sequence containing the number of sub- and
super-diagonals within the band of the Jacobi matrix, the
Jacobi matrix is considered banded (only for ``fprime=None``).
epsfcn : float, optional
A suitable step length for the forward-difference
approximation of the Jacobian (for ``fprime=None``). If
`epsfcn` is less than the machine precision, it is assumed
that the relative errors in the functions are of the order of
the machine precision.
factor : float, optional
A parameter determining the initial step bound
(``factor * || diag * x||``). Should be in the interval
``(0.1, 100)``.
diag : sequence, optional
N positive entries that serve as a scale factors for the
variables.
Returns
-------
x : ndarray
The solution (or the result of the last iteration for
an unsuccessful call).
infodict : dict
A dictionary of optional outputs with the keys:
``nfev``
number of function calls
``njev``
number of Jacobian calls
``fvec``
function evaluated at the output
``fjac``
the orthogonal matrix, q, produced by the QR
factorization of the final approximate Jacobian
matrix, stored column wise
``r``
upper triangular matrix produced by QR factorization
of the same matrix
``qtf``
the vector ``(transpose(q) * fvec)``
ier : int
An integer flag. Set to 1 if a solution was found, otherwise refer
to `mesg` for more information.
mesg : str
If no solution is found, `mesg` details the cause of failure.
See Also
--------
root : Interface to root finding algorithms for multivariate
functions. See the ``method=='hybr'`` in particular.
Notes
-----
``fsolve`` is a wrapper around MINPACK's hybrd and hybrj algorithms.
Examples
--------
Find a solution to the system of equations:
``x0*cos(x1) = 4, x1*x0 - x1 = 5``.
>>> from scipy.optimize import fsolve
>>> def func(x):
... return [x[0] * np.cos(x[1]) - 4,
... x[1] * x[0] - x[1] - 5]
>>> root = fsolve(func, [1, 1])
>>> root
array([6.50409711, 0.90841421])
>>> np.isclose(func(root), [0.0, 0.0]) # func(root) should be almost 0.0.
array([ True, True])关键字参数: full_output=True
多项式的复数根 :np.roots([最高位系数,次高位系数,... ... x项系数,常数项])
>>>f = lambda x:x**4 + x -1
>>>np.roots([1,0,0,1,-1])
>>>array([-1.22074408+0.j , 0.24812606+1.03398206j,
0.24812606-1.03398206j, 0.72449196+0.j ])- 求解线性等式 scipy.linalg
- 利用dir()获取常用函数

import numpy as np import scipy.linalg as sla from scipy.linalg import inv a = np.array([-1,5]) c = np.array([[1,3],[3,4]]) x = np.dot(inv(c),a) >>>x >>>array([ 3.8, -1.6])
数值积分 scipy.integrate
- 利用dir()获取你需要的信息
- 对自定义函数做积分

import scipy.integrate as si
from scipy.integrate import quad
import numpy as np
import matplotlib.pyplot as plt
f = lambda x:x**1.05*0.001
interval = 100
xmax = np.linspace(1,5,interval)
integral,error = np.zeros(xmax.size),np.zeros(xmax.size)
for i in range(interval):
integral[i],error[i] = quad(f,0,xmax[i])
plt.plot(xmax,integral,label="integral")
plt.plot(xmax,error,label="error")
plt.show()对震荡函数做积分
quad 函数允许 调整他使用的网格
>>>(-0.4677718053224297, 2.5318630220102742e-05) >>>quad(np.cos,-1,1,limit=100) >>>(1.6829419696157932, 1.8684409237754643e-14) >>>quad(np.cos,-1,1,limit=1000) >>>(1.6829419696157932, 1.8684409237754643e-14) >>>quad(np.cos,-1,1,limit=10) >>>(1.6829419696157932, 1.8684409237754643e-14)
微分方程的数值解 参见 Python数值求解微分方程方法(欧拉法,隐式欧拉)
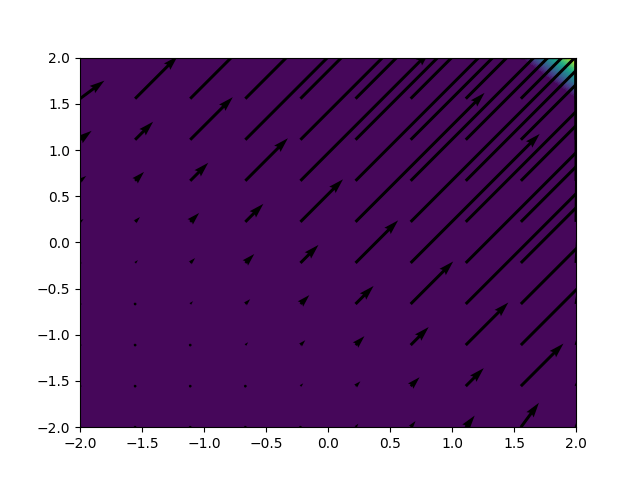
向量场与流线图:
vector(x,y) = (y,-x)
import numpy as np import matplotlib.pyplot as plt coords = np.linspace(-1,1,30) X,Y = np.meshgrid(coords,coords) Vx,Vy = Y,-X plt.quiver(X,Y,Vx,Vy) plt.show() ------------------ import numpy as np import matplotlib.pyplot as plt coords = np.linspace(-2,2,10) X,Y = np.meshgrid(coords,coords) Z = np.exp(np.exp(X+Y)) ds = 4/6 dX,dY = np.gradient(Z,ds) plt.contourf(X,Y,Z,25) plt.quiver(X,Y,dX.transpose(),dY.transpose(),scale=25) plt.show()

到此这篇关于Python数值方法及数据可视化的文章就介绍到这了,更多相关Python数值 视化内容请搜索好代码网以前的文章或继续浏览下面的相关文章希望大家以后多多支持好代码网!