题目描述
打印杨辉三角(前N行)
问题分析
杨辉三角是中国古代数学的杰出研究成果之一,它把二项式系数图形化,把组合数内在的一些代数性质直观地从图形中体现出来,是
题目描述
打印杨辉三角(前N行)
问题分析
杨辉三角是中国古代数学的杰出研究成果之一,它把二项式系数图形化,把组合数内在的一些代数性质直观地从图形中体现出来,是一种离散型的数与形的结合。
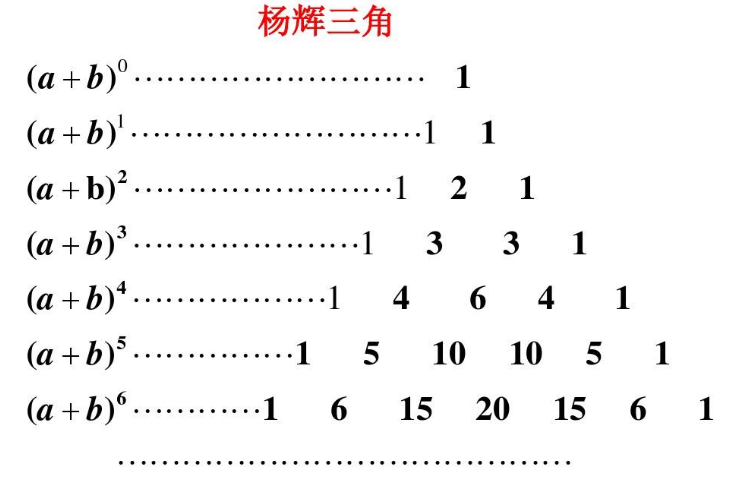
杨辉三角的部分规律:
- 每个数等于它上方两数之和。
- 每行数字左右对称,由1开始逐渐变大。
- 第n行的数字有n项。
- 第n行的m个数可表示为 C(n-1,m-1),即为从n-1个不同元素中取m-1个元素的组合数。
根据前三个规律,我们可以使用数组法获取杨辉三角;根据后两个规律,我们可以使用公式法求出每行每列的数字。
数组法思路:先根据设定的行数定义一个二维数组,然后使用一个双层循环,外层循环的因数为杨辉三角的行数,内层循环用来将杨辉三角每行的数字存入数组。每行第一列和最后一列都是1,中间的数字等于它上方两数之和。
最后再通过两层循环将二维数组中的数字打印。
公式法思路:由于杨辉三角满足上面提到的第4点规律,所以我们可以直接定义一个函数求出杨辉三角第n行的m个数的值。
组合数公式

根据上面这个组合的公式,我们可以使用阶乘及相关计算,求出杨辉三角形的每个数,同时打印出来。
1. 使用数组法(打印直角三角)
打印直角形式的杨辉三角形,即打印二维数组时不加空格
代码
#include <stdio.h>
#define LINE_MAXIMUM 10 //行数
int main()
{
int i = 0, j = 0;
int array[LINE_MAXIMUM][LINE_MAXIMUM] = {0};
/* 填充二维数组 */
for(i = 0; i < LINE_MAXIMUM; i++) //行数
{
for(j = 0; j <= i; j++) //每行的列数(第n行的数字有n项)
{
if(j == 0 || j == i) //每行第一列和最后一列为1
array[i][j] = 1;
else //每个数等于它上方两数之和
array[i][j] = array[i - 1][j - 1]\
+ array[i - 1][j];
}
}
/* 打印杨辉三角(直角) */
for(i = 0; i < LINE_MAXIMUM; i++)
{
for(j = 0; j <= i; j++)
printf("%d ", array[i][j]);
printf("\n");
}
return 0;
}
运行结果

2. 使用数组法(打印等腰三角)
打印等腰形式的杨辉三角形,需要在每行前面加若干空格,空格的宽度需要根据数字的宽度调整,使三角形对称。
代码
#include <stdio.h>
#define LINE_MAXIMUM 10 //行数
int main()
{
int i = 0, j = 0;
int array[LINE_MAXIMUM][LINE_MAXIMUM] = {0};
int k = 0;
/* 填充二维数组 */
for(i = 0; i < LINE_MAXIMUM; i++) //行数
{
for(j = 0; j <= i; j++) //每行的列数(第n行的数字有n项)
{
if(j == 0 || j == i) //每行第一列和最后一列为1
array[i][j] = 1;
else //每个数等于它上方两数之和
array[i][j] = array[i - 1][j - 1]\
+ array[i - 1][j];
}
}
/* 打印杨辉三角(等腰) */
for(i = 0; i < LINE_MAXIMUM; i++)
{
//在数字前打印空格,最后一行空格数为0
for(k = 1; k < LINE_MAXIMUM - i; k++)
printf(" ");
for(j = 0; j <= i; j++)
printf("%3d ", array[i][j]);
printf("\n");
}
return 0;
}
运行结果

3. 使用公式法(打印等腰三角)
由于循环都是从 0 开始,所以核心函数的功能是获取杨辉三角第 m + 1 行,第 n + 1 个数的值(行数最小为1),即求C(m,n)。另外,由于公式中存在除法,所以行数列数及结果不能使用整型,需要用浮点型。
代码
#include<stdio.h>
#define LINE_MAXIMUM 10 //行数
/**
* @brief 获得阶乘结果(递归实现)
* @param num 输入的参数
* @return 返回num!(阶乘)
*/
float Get_Factorial(float num)
{
if(num >= 1)
return num * Get_Factorial(num - 1);
else //0! = 1
return 1;
}
//获取杨辉三角第 m + 1 行,第 n + 1 个数的值为 C(m,n)
float Get_Num(float m, float n)
{
return Get_Factorial(n) / Get_Factorial(m) / Get_Factorial(n - m) ;
}
int main()
{
float i = 0, j = 0, k = 0;
/* 打印杨辉三角(等腰) */
for(i = 0; i < LINE_MAXIMUM; i++)
{
//在数字前打印空格,最后一行空格数为0,第一行为空格数为LINE_MAXIMUM - 1
for(k = 1; k < LINE_MAXIMUM - i; k++)
printf(" ");
for(j = 0; j <= i; j++)
printf("%3.0f ", Get_Num(j, i));
printf("\n");
}
return 0;
}
运行结果

网上参考
这份代码看起来很简洁,使用的是公式法。
#include <stdio.h>
#include <stdlib.h>
int main()
{
int s = 1, h; // 数值和高度
int i, j; // 循环计数
scanf("%d", &h); // 输入层数
printf("1\n"); // 输出第一个 1
for (i = 2; i <= h; s = 1, i++) // 行数 i 从 2 到层高
{
printf("1 "); // 第一个 1
for (j = 1; j <= i - 2; j++) // 列位置 j 绕过第一个直接开始循环
printf("%d ", (s = (i - j) * s / j));
printf("1\n"); // 最后一个 1,换行
}
getchar(); // 暂停等待
return 0;
}
到此这篇关于C语言实现打印杨辉三角的方法详细(两种方法)的文章就介绍到这了,更多相关C语言打印杨辉三角内容请搜索好代码网以前的文章或继续浏览下面的相关文章希望大家以后多多支持好代码网!