1 二叉树的概念及结构
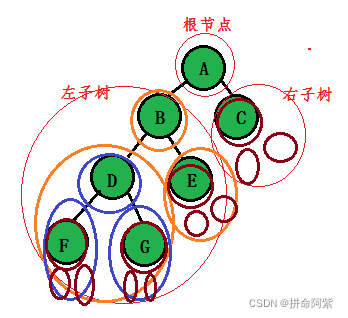
①概念:一棵二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
②二叉树的特点:
1.二叉树的概念及结构
①概念:一棵二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
②二叉树的特点:
- 每个结点最多有两棵子树,即二叉树不存在度大于2的结点。(度最多为2)
- 二叉树的子树有左右之分,其子树的次序不能颠倒。
③现实中的二叉树:

当一名普通的人看到这样一颗树,可能会想:好标准的一棵树
当一个程序猿看到这样一棵树,可能会想:好像数据结构中的二叉树,并且还是颗满二叉树
④数据结构中的二叉树:
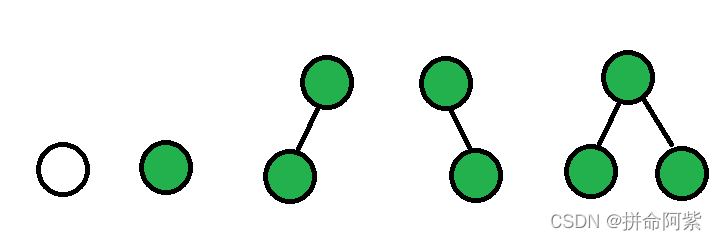
注:二叉树最多有两个度
⑤特殊的二叉树:
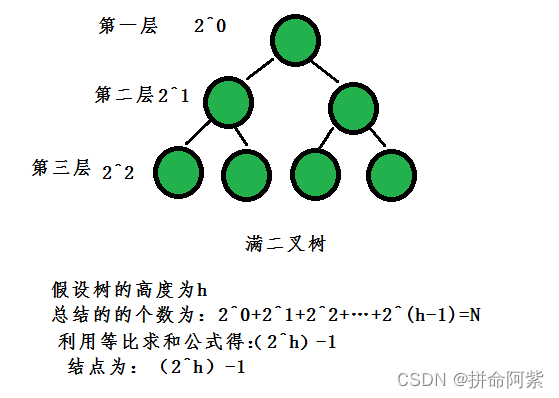
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉 树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。
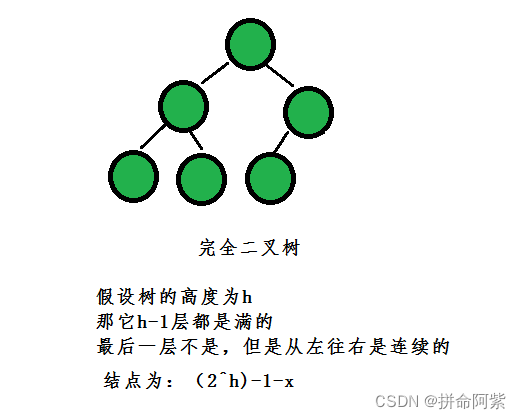
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对 于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号 从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉 树。
⑥二叉树的存储结构: 二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
⑦二叉树的性质:
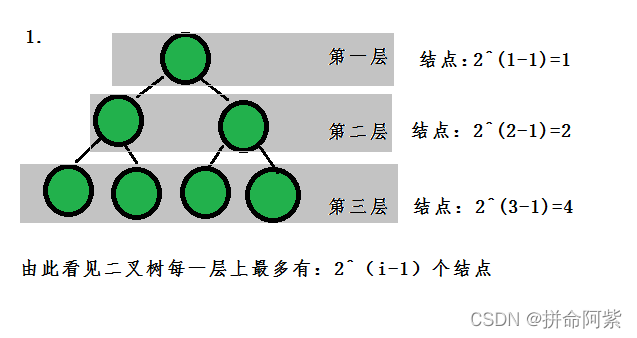
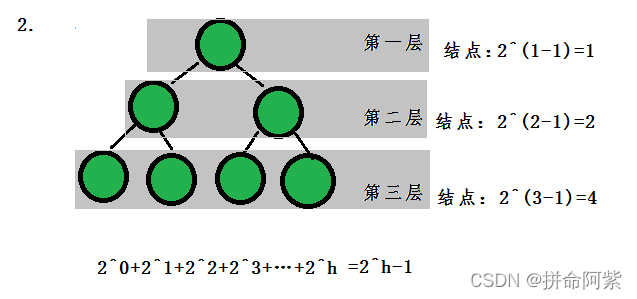
- 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1) 个结点.
- 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h- 1.
- 对任何一棵二叉树, 如果度为0其叶结点个数为 n0, 度为2的分支结点个数为 n2,则有n0=n2 +1
- 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=log₂n+1
⑧练习题



2.二叉树链式结构的实现
①二叉树链式结构的遍历 :
所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访 问结点所做的操作依赖于具体的应用问 题。 遍历是二叉树上最重要的运算之一,是二叉树上进行 其它运算之基础。
前序/中序/后序的递归结构遍历:是根据访问结点操作发生位置命名
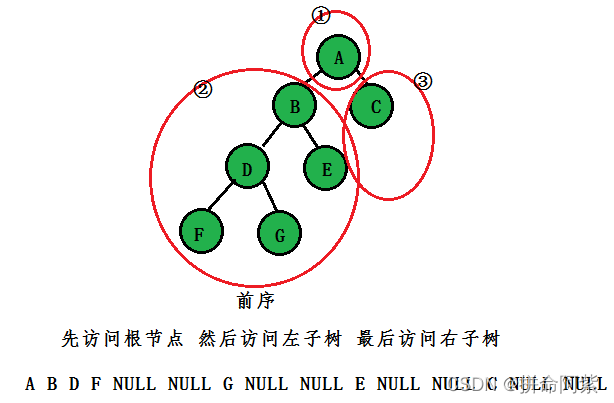
- 前序(先根):先访问根节点,然后访问左子树,最后访问右子树
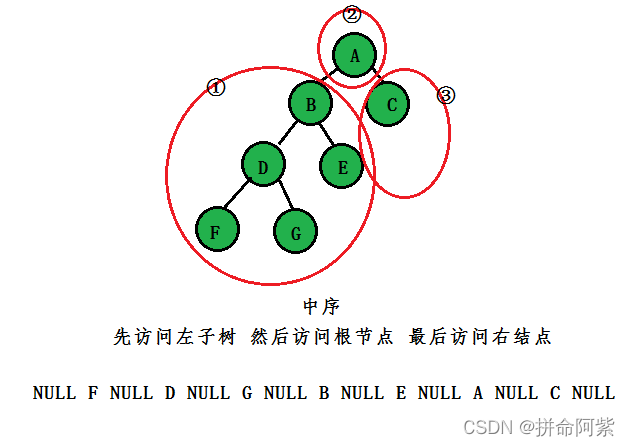
- 中序(中根):先访问左节点,然后访问根节点,最后访问右子树
- 后序(后根):先访问左节点,然后访问右子树,最后访问根节点

先定一个结构体类型:
typedef char BTDataType;
typedef struct BinarytreeNode
{
BTDataType data;
struct BinarytreeNode* left;
struct BinarytreeNode* right;
}BTNode;前序:
void Preamble(BTNode* p)//前序
{
if (p == NULL)
{
printf("NULL ");
return;
}
printf("%c ", p->data);
Preamble(p->left);
Preamble(p->right);
}中序:
void Morder(BTNode* p)//中序
{
if (p == NULL)
{
printf("NULL ");
return;
}
Morder(p->left);
printf("%c ", p->data);
Morder(p->right);
}后序:
void Porder(BTNode* p)//后序
{
if (p == NULL)
{
printf("NULL ");
return;
}
Porder(p->left);
Porder(p->right);
printf("%c ", p->data);
}求二叉树结点的个数:
int treeSize(BTNode* p)//结点个数
{
return p == NULL ? 0 : treeSize(p->left) + treeSize(p->right)+1;
}求叶子结点的个数:
int treeLeafSize(BTNode* p)//叶子结点个数
{
if (p == NULL)
{
return 0;
}
if (p->left == NULL&&p->right == NULL)
{
return 1;
}
return treeLeafSize(p->left) + treeLeafSize(p->right);
}到此这篇关于C语言 超详细总结讲解二叉树的概念与使用的文章就介绍到这了,更多相关C语言 二叉树内容请搜索好代码网以前的文章或继续浏览下面的相关文章希望大家以后多多支持好代码网!