数据类型的介绍
在前面的章节中我们基本认识到了各种数据类型,这里我们就稍微回忆以下吧
类型的意义:
- 决定了访问内存空间的大小
- 决定了看待内存空间的视角(例如:整型和字符数据类型)
类型的基本归类
整型家族:
char
unsigned char
signed char
short
unsigned short [int]
signed short [int]
int
unsigned int
signed int
long
unsigned long [int]
signed long [int]
浮点型家族:
float
double
构造类型:
> 数组类型
> 结构体类型 struct
> 枚举类型 enum
> 联合类型 union
指针类型:
int *pi; char *pc; float *pf; void *pv;(泛型指针)
空类型:
void 表示空类型 (无类型)
通常用于 函数的返回类型、函数的参数、指针类型
//作为函数的返回类型
void f1()//不接受任何返回值
{
;
}
//作为函数的参数
int f2(void)//参数为void时,传入参数会报错
{
;
}
//作为指针类型
void* f3(void* pv)//参数为 void* 时,可接收任意类型的参数
{
;
}整型在内存中的存储
计算机中的整数有三种2进制表示方法,即源码、反码、补码。
三种表示方法均有符号位和数值位
符号位: " 0 " 表示 正," 1 "表示 负
数值位:
正数:
原码、反码、补码相同
负数:
原码:直接将数值按二进制翻译
反码:原码符号位不变,其它位按位取反
补码:反码+1
我们可以在内存中的存储看到:
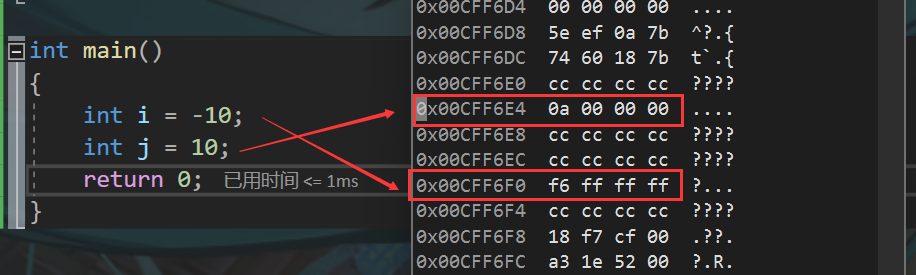
这里大家可能有个疑问,为什么j 和i在内存中会是这样?为什么i 和 j内部二进制会倒过来存储呢??编译器坏了?(bushi
如果对此事好奇,就接着往下看吧。
什么是大小端
大小端存储是计算机的一种存储方式,其主存储的方式也由计算机决定。
什么是大小端存储:
大端(存储)模式:指的是,数据的低 (二进制)位保存在高地址中,高位保存在低地址中;
小端(存储)模式:指的是,数据的低位保存在低地址中,高位保存在高地址中;
注意:
大小端存储只跟单个类型数据的存储方式有关,数组的存储依然是由低地址向高地址进行存储
浮点数在内存中的存储
在认识浮点数在内存中的存储之前,我们先看一下下面的例子:
int main()
{
int n = 9;
float* pf = (float*)&n;
printf("n的值为:%d\n", n);
printf("pf的值为:%f\n", *pf);
*pf = 9.0;
printf("n的值为:%d\n", n);
printf("pf的值为:%f\n", *pf);
return 0;
}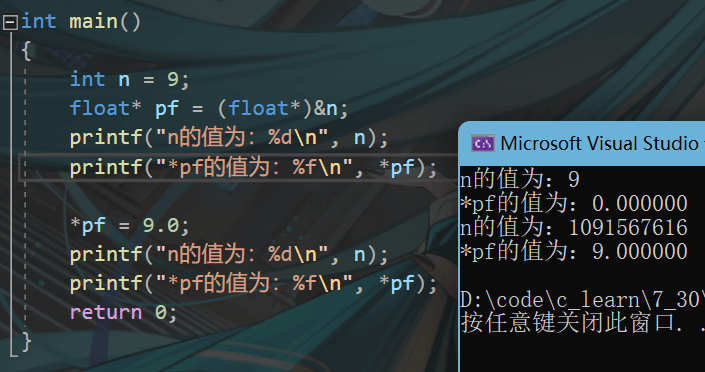
为什么输出结果会是这样?
想要了解其中的原因我们首先要知道浮点数在内存中的存储规则
浮点数在内存中的存储规则
浮点数存储根据国际标准 IEEE (电气工程师学会) 754 来进行存储,具体规则如下:
- (-1)^S * M * 2^E
- (-1)^S 代表 符号位,S=0为正数,S=1为负数
- M 表示有效数字,(1 ≤ M < 2)
- 2^E表示指数位
IEEE 754规定:
对于 float 类型来说:

对于 double 类型来说:

IEEE 754对 有效数字M 和 指数E 有一些特殊的规定:
有效数字M
前面说过,1 ≤ M < 2,也就是说,M可以写成 1.xxxxxx 的形式,将 小数点前省略,则其中xxxxxx 就是我们所要保存的数字
指数E
对于 float 类型(E 占 8 位):E + 127 (取 0~255 中间数)
对于 double 类型(E 占 11 位):E + 1023 (取 0~2047 中间数)
举个例子(o゚v゚)ノ
十进制的 5.0 想要存进去
小数点前 需要转换成 二进制 101 . 0
根据科学计数法将其转换,1.01 x 2^(2)
指数E 进行替换 E = 2+127 = 129 = 1000 0001(二进制)
由上可得出 S = 0 E = 1000 0001 M = 1.01
0 10000001 01000000000000000000000
S E M整理一下:
0100 0000 1010 0000 0000 0000 0000 0000
用十六进制表示:
4 0 a 0 0 0 0 0
整理一下:(大端存储)
40 a0 00 00
小端存储:
00 00 a0 40

趁着手还热乎,赶紧再来看看吧(/≧▽≦)/
十进制 -2.25 在内存中如何存储?
- 符号为负
S = 1 - 小数点前正着写二进制,小数点后按照
2^(-n),n = 4 (1/4=0.25),(倒着写二进制),所以二进制为10.01 - 用科学计数表示
1.001 x 2^(1) - 指数E进行替换
E = 1 + 127 = 128 = 1000 0000(二进制) - 由上可得
S = 1E = 1000 0000M = 1.001
1 10000000 00100000000000000000000
S E M整理一下:
1100 0000 0001 0000 0000 0000 0000 0000
用十六进制表示:
c 0 1 0 0 0 0 0
整理一下:
c0 10 00 00
小端存储:
00 00 10 c0
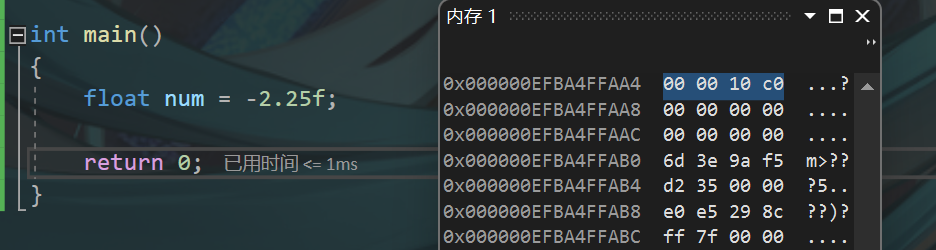
注意:(特殊情况)
当指数E为边界值时 0~255(0~1023)直接等于具体的真实值
E全为0:
直接等于0
E全为1:
直接等于具体值340282346638528859811704183484516925440.000000(2^255)
到此这篇关于C语言数据存储归类介绍的文章就介绍到这了,更多相关C语言数据存储内容请搜索好代码网以前的文章或继续浏览下面的相关文章希望大家以后多多支持好代码网!